NCERT Solutions for Class 8th Maths Chapter 1 Rational Numbers

 

NCERT Solutions for Class 8 Maths 

Chapter 1 Rational Numbers

Exercise 1.1

Q1.
Using appropriate properties find: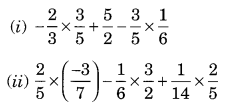

Sol:

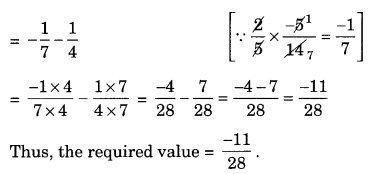
Q2.
Write the additive inverse of each of the following:
(i) 28
(ii) −59
(iii) −6−5
(iv) 2−9
(v) 19−6
Sol:

Q3.
Verify that -(-x) = x for
(i) x = 115
(ii) x = −1317
Sol: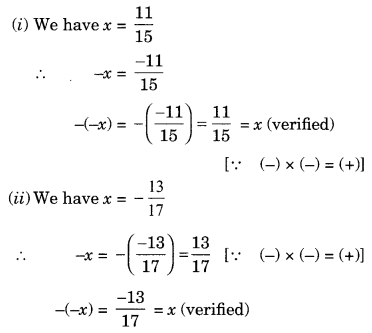

 Q4.
Find the multiplicative inverse of the following: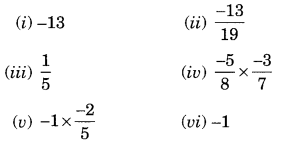

Sol: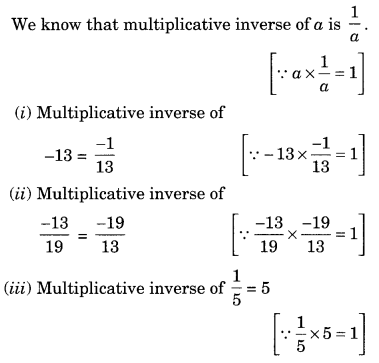

Q5.
Name the property under multiplication used in each of the following: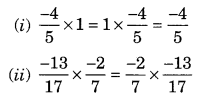

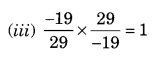
Sol:
(i) Commutative property of multiplication
(ii) Commutative property of multiplication
(iii) Multiplicative inverse property

Q6.
Multiply 613 by the reciprocal of −716.
Sol: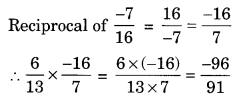

Q7.
Tell what property allows you to compute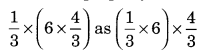

Sol:
Since a × (b × c) = (a × b) × c shows the associative property of multiplications.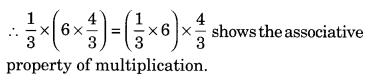

 Q 8.

Is 89 the multiplicative inverse of -118? Why or Why not?
Sol:
Here -118 = −98.
Since multiplicative inverse of 89 is 98 but not −98
89 is not the multiplicative inverse of -118

 Q9.
If 0.3 the multiplicative inverse of 313? Why or why not?
Sol: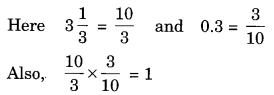

Multiplicative inverse of 0.3 or 310 is 103.
Thus, 0.3 is the multiplicative inverse of 313.

 Q10.
Write:
(i) The rational number that does not have a reciprocal.
(ii) The rational numbers that are equal to their reciprocals.
(iii) The rational number that is equal to its negative.
Solution:
(i) 0 is the rational number which does not have its reciprocal
[∵ 10 is not defined]
(ii) Reciprocal of 1 = 11 = 1
Reciprocal of -1 = 1−1 = -1
Thus, 1 and -1 are the required rational numbers.
(iii) 0 is the rational number which is equal to its negative.

Q11.
Fill in the blanks.
(i) Zero has ……….. reciprocal.
(ii) The numbers ……….. and ……….. are their own reciprocals.
(iii) The reciprocal of -5 is ………
(iv) Reciprocal of 1x, where x ≠ 0 is ……….
(v) The product of two rational numbers is always a …………
(vi) The reciprocal of a positive rational number is ……….
Sol:
(i) no
(ii) -1 and 1
(iii) −15
(iv) x
(v) rational number
(vi) positive